Matrices in Ruby
This semester, I have taken on a module taught using Python + numpy + various packages, which I am learning as I go. In this and later posts, I shall explore how the Python stuff can be replicated in Ruby.
I am not interested in "notebook" environments. My explorations will be
conducted in irb.
1. Matrices
Ruby has a matrix library, built-in. However, for faster performance, other libraries are available: I shall use numo-narray-alt and numo-linalg-alt. These libraries are supported by yoshoku, the developer of the Ruby machine-learning library rumale.
Once installed:
irb(main):001> require "numo/narray" => true irb(main):003> Numo::NArray::VERSION => "0.10.0"
1.1. Creating arrays
A numo array can be created from a Ruby array:
irb(main):006> a = Numo::NArray[1,3,6,10] => Numo::Int32#shape=[4] ... irb(main):007> p a Numo::Int32#shape=[4] [1, 3, 6, 10] => Numo::Int32#shape=[4] [1, 3, 6, 10]
Creating a 1D and 2D array of random integers:
irb(main):020> Numo::Int32.new(4).rand(5) => Numo::Int32#shape=[4] [3, 4, 2, 4] irb(main):021> Numo::Int32.new(2,3).rand(5) => Numo::Int32#shape=[2,3] [[2, 4, 3], [3, 0, 3]]
1.2. Array indexing
(output has been abbreviated)
# create sequence of 12 integers irb(main):035> c = Numo::Int32.new(12).seq # extract first four elements irb(main):036> c[0...4] [0, 1, 2, 3] irb(main):037> c[0..3] [0, 1, 2, 3] # extract every other element from first four elements irb(main):038> c[(0..3).step(2)] [0, 2] # extract every third element, starting from first irb(main):039> c[(0..).step(3)] [0, 3, 6, 9] # extract every other element, starting from second irb(main):040> c[(1..).step(2)] [1, 3, 5, 7, 9, 11] # extract elements in reverse, from index 5 irb(main):044> c[(0..5)].reverse [5, 4, 3, 2, 1, 0]
Similarly for multi-dimensional slices:
irb(main):045> x = Numo::Int32.new(3,4).rand(12) => Numo::Int32#shape=[3,4] [[11, 0, 1, 5], [9, 2, 1, 7], [10, 10, 3, 0]] irb(main):052> x[1...2,0...2] => Numo::Int32(view)#shape=[1,2] [[9, 2]]
1.3. Reshaping/splitting/joining arrays
Reshaping lets us convert a 1D array into a 2D one:
irb(main):057> d = c.reshape(3,4) irb(main):058> d Numo::Int32#shape=[3,4] [[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]]
For combining matrices, there is concatenate, using axis to control which
dimension the concatenation is performed along:
irb(main):095> a = Numo::Int32[[1,2], [3,4]] irb(main):096> b = Numo::Int32[[5,6]] irb(main):097> a [[1, 2], [3, 4]] irb(main):098> b [[5, 6]] irb(main):099> a.concatenate(b) [[1, 2], [3, 4], [5, 6]] irb(main):101> a.concatenate(b.transpose, axis:1) [[1, 2, 5], [3, 4, 6]]
For dividing matrices, there is split, again using axis to determine
how the matrix is subdivided:
irb(main):075> d [[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]] irb(main):103> d.split(2) # axis:0 => [Numo::Int32(view)#shape=[2,4] [[0, 1, 2, 3], [4, 5, 6, 7]], Numo::Int32(view)#shape=[1,4] [[8, 9, 10, 11]]] irb(main):104> d.split(2, axis:1) => [Numo::Int32(view)#shape=[3,2] [[0, 1], [4, 5], [8, 9]], Numo::Int32(view)#shape=[3,2] [[2, 3], [6, 7], [10, 11]]]
1.4. Scalar operations
These are applied to individual elements of the array, preserving its structure:
irb(main):105> a = Numo::Int32[10, 15, -2, 9] irb(main):107> b = Numo::Int32.new(4).seq irb(main):110> 2*a [20, 30, -4, 18] irb(main):111> a*2 [20, 30, -4, 18] irb(main):112> b**2 [0, 1, 4, 9] irb(main):122> a.abs [10, 15, 2, 9] irb(main):123> a+4 [14, 19, 2, 13] irb(main):124> a-3 [7, 12, -5, 6] irb(main):125> -a [-10, -15, 2, -9] irb(main):126> a % 2 [0, 1, 0, 1]
1.5. Operations on two matrices
irb(main):108> a+b [10, 16, 0, 12] irb(main):109> a-b [10, 14, -4, 6] irb(main):127> a.gt b [1, 1, 0, 1] irb(main):129> a.ge b [1, 1, 0, 1] irb(main):132> a.lt b [0, 0, 1, 0] irb(main):133> a.le b [0, 0, 1, 0]
The comparison operations, like gt, return 1 if the corresponding elements
match the condition, else 0.
In the following, notice that * performs element-wise multiplication and
dot performs matrix multiplication:
irb(main):002> a = Numo::Int32[[2,3],[5,-8]] irb(main):003> b = Numo::Int32[[1,-4],[8,-6]] irb(main):004> a+b [[3, -1], [13, -14]] irb(main):005> a*b [[2, -12], [40, 48]] irb(main):006> a.dot b [[26, -26], [-59, 28]]
1.6. Single matrix operations
These take a matrix and convert it to another matrix or scalar:
irb(main):117> m = Numo::Int32[[2,3],[5,-8]] irb(main):118> m.sum => 2 irb(main):119> m.min => -8 irb(main):120> m.max => 5 irb(main):129> m.diagonal [2, -8] irb(main):130> m.trace => -6
and, using the numo-linalg-alt library:
irb(main):002> require "numo/linalg" irb(main):004> Numo::Linalg.inv(m) => Numo::DFloat#shape=[2,2] [[0.258065, 0.0967742], [0.16129, -0.0645161]] irb(main):005> Numo::Linalg.det(m) => -31.0
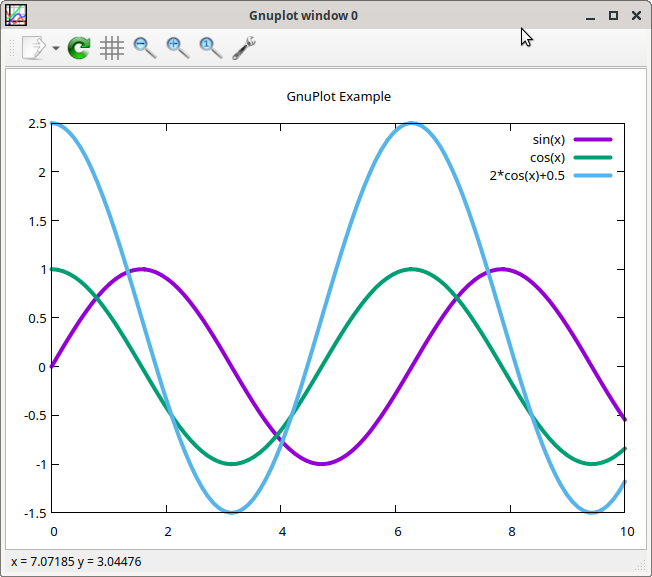
2. Graph Plotting
The final part was about plotting a graph using matplotlib, for
which Ruby is well served by the gnuplot gem:
require "gnuplot"
Gnuplot.open do |gp|
Gnuplot::Plot.new( gp ) do |plot|
plot.xrange "[0:10]"
plot.title "GnuPlot Example"
plot.data << Gnuplot::DataSet.new( "sin(x)" ) do |ds|
ds.with = "lines"
ds.linewidth = 4
end
plot.data << Gnuplot::DataSet.new( "cos(x)" ) do |ds|
ds.with = "lines"
ds.linewidth = 4
end
plot.data << Gnuplot::DataSet.new( "2*cos(x)+0.5" ) do |ds|
ds.with = "lines"
ds.linewidth = 4
end
end
end